In his book Thinking Fast and Slow, Daniel Kahneman gives an example of elementary Bayesian inference, posing this question:
"A cab was involved in a hit-and-run accident at night. Two cab companies, the Green and the Blue, operate in the city. You are given the following data: 85% of the cabs in the city are Green and 15% are Blue. A witness identified the cab as Blue. The court tested the reliability of the witness under the circumstances that existed on the night of the accident and concluded that the witness correctly identified each one of the two colors 80% of the time and failed 20% of the time. What is the probability that the cab involved in the accident was Blue rather than Green?"Kahneman goes on to observe that "The two sources of information can be combined by Bayes's rule. The correct answer is 41%. However, you can probably guess what people do when faced with this problem: they ignore the base rate and go with the witness. The most common answer is 80%."
So why is the correct answer 41%?
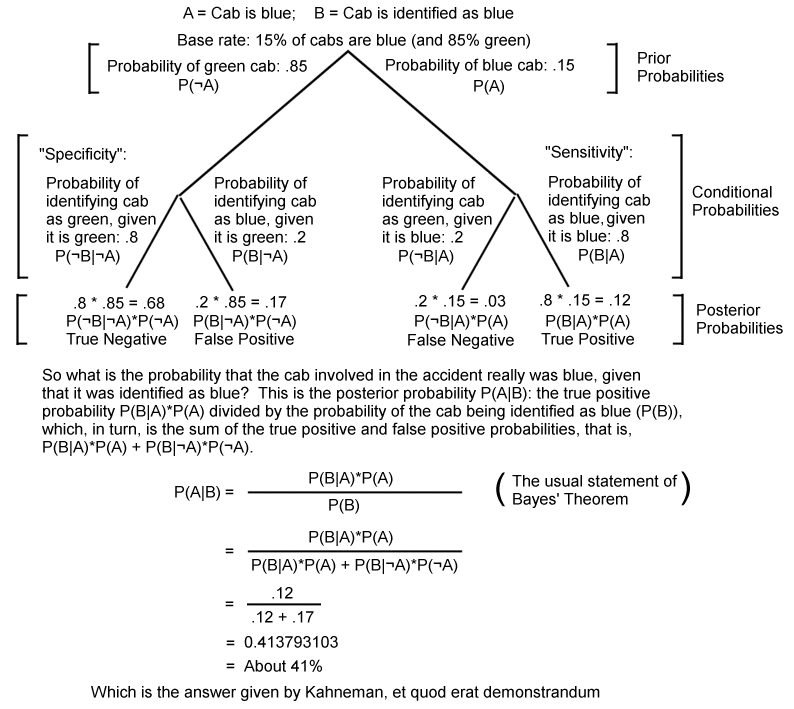
The image illustrates Bayes' Theorem using a tree diagram. At the top, there are two branches. The right branch, "Cab is blue," has a probability of .15, 15%. The left branch, "Cab is Green," has a probability of .85, 85%. These are the "prior probabilities," and represent what the chance of a cab being blue or green would be, if the cab were randomly selected from all cabs in the city. On the right branch, "Cab is blue", there is another split into two branches. The right branch here shows the conditional probability of the witness correctly identifying the cab as blue, if it was blue. That number is .8, 80%. Multiplying .15 by .8 gives us .12, 12%, which is the posterior probability of the accident involving a blue cab that was correctly identified as blue, a "true positive". The left branch at this level shows the probability of the witness identifying the cab as green, given it was really blue. This probability is just one, minus .8, that is, .2. Multiplying .15 by .2 gives us .03, 3%, which is the posterior probability of the accident involving a blue cab mistakenly identified as green. This is a "false negative."
Following the left branch from the top of the diagram, "Cab is green," there is a similar split. Here the left branch shows the conditional probability of the witness correctly identifying the cab as green, if it was green. As on the other side of the tree, that number is .8, 80%. Multiplying .85 by .8 gives us .68, 68%, which is the posterior probability of the accident involving a green cab that was correctly identified as green, a "true negative". The right branch at this level shows the probability of the witness mistakenly identifying the cab as blue, given it was really green. Again, this probability is just one, minus .8, that is, .2. Multiplying .85 by .2 gives us .17, 17%, which is the posterior probability of the accident involving a green cab mistakenly identified as blue. This is a "false positive."
The true positive and false positive probabilities can be combined, using Bayes's Theorem, to give us the answer given by Kahneman. To give the probability that the accident cab was really blue, if identified as such by the witness, we divide the true positive probability by the sum of the true positive and false positive probabilities. This is .12 divided by .12 plus .17, which computes as .4138, or about 41%, as Kahneman said.
The result is surprising to some, but the reason is easy to understand: even though the witness identifies cab colors with 80% accuracy, there are so many more green cabs than blue that the chance of mistaken identification outweighs the chance of correct identification. This also works the other way. If the percentages of green and blue cabs were reversed, so that 85% of the cabs were blue and 15% green, the probability that the accident cab was blue, and was correctly identified as such, would rise to 96%. If half the cabs in the city were green and half blue, then the base rate would be uninformative in this example, and the chance of a correct identification would be 80%. You can try these and other scenarios using the calculator below.
Calculator
Bayes' Theorem is easy to understand when shown graphically, as above. Click here to run the calculator for Kahneman's example, or enter the values yourself above. (Calculator accepts arguments by query string, e.g. https://anesi.com/bayes.htm?p_a=.15&p_b_a=.8&p_not_b_not_a=.8)
The active charts produced by the calculator are intended to illustrate the rather non-inituitive (for most of us) interplay of sensitivity, specificity, and prevalence. Mouse or thumb over the active chart to show actual values. Charting is done with the Highcharts JavaScript library, which we highly recommend (click the hamburger icon on a chart for print, image or pdf download options).
Positive Predictive Value (PPV) is the value Kahneman was looking for in his example — true positives divided by the sum of true positives and false positives. In his cab example, this is the probability of a cab being blue, given it was identified as blue. In a diagnostic test, the probability of having the disease, given a positive diagnostic test. Kahneman's point was that this is usually confused with sensitivity, which is the reverse — the probability of identifying the cab as blue, given it was blue, or the probability of a positive diagnostic test, given you have the disease. To get PPV, you need to know the base rate (prevalence). But sensitivity has nothing to do with the base rate, it's just an attribute of the test.
Negative Predictive Value (NPV), also useful, is true negatives divided by the sum of true negatives and false negatives. In the cab example, this is the probability of a cab being green (not blue), given it was identified as green (not blue). In a diagnostic test, the probability of not having the disease, given a negative diagnostic test. This can be confused with specificity, which is the reverse — the probability of identifying the cab as green, given it was green, or the probability of a negative diagnostic test, given you do not have the disease. To get NPV, you need to know the base rate (prevalence). But specificity has nothing to do with the base rate, it's just an attribute of the test.
Wikipedia has an article treating these matters in much greater and better detail than we can provide here. Already spent way more time on this then I intended to.
(While prevalence is important in most cases, in some edge cases it obviously is not. If specificity is 1 then PPV is 1, as false positives are impossible; if sensitivity is 1 then NPV is 1, because false negatives are impossible; if prevalence is .5 and specificity and sensitivity are equal, then PPV, NPV, sensitivity, and specificity are equal; PPV and NPV are undefined if sensitivity and specificity are 0 and 1 or 1 and 0, respectively; etc. But these are unusual and uninteresting cases.)
Application to Coronavirus Testing
If Kahneman decides to revise Thinking Fast and Slow, he can replace his taxicab hypothetical with a coronavirus hypothetical. Like this:A coronavirus epidemic strikes the United States. In mid-March, about 1% of the population has been infected.1 Acme Therapeutics has created an antibody test for the virus. Research shows that if a person has antibodies, the test will give a positive result 99% of the time2, and a negative result 1% of the time.3 If a person does not have antibodies, the test will give a negative result 99% of the time4, and a positive result 1% of the time.5 If a person gets a positive test result, what is the probability that he has antibodies?6Well it’s sure not 99%. The correct answer — the positive predictive value, the probability of having antibodies given a positive test — is 50%.1 Prevalence, or base rate.
2 Sensitivity, or true positive rate
3 False negative rate
4 Specificity, or true negative rate
5 False positive rate
6 Positive predictive value (PPV) or precision
Intuitive explanation: If nobody in the population has the virus, then all positive test results are false positives, because by definition a true positive can occur only when someone has the virus. If everybody in the population has the virus, then all positive test results are true positives, because by definition a false positive can occur only when someone does not have the virus. Between these extremes, the proportion of positive results that are true positives — the positive predictive value — increases gradually from zero to 100%. How?
Positive predictive value is just true positives (Sensitivity x Prevalence) divided by the sum of true positives (Sensitivity x Prevalence) and false positives ((1 – Prevalence) x (1 – Specificity)). You can do the arithmetic yourself, or just use the calculator. The calculator will also display an active chart showing how PPV increases, rapidly in this example, as prevalence increases. With a sensitivity and specificity of 99%, PPV hits 95% when prevalence is 17%.
So population prevalence is very important when intepreting an individual's test results.
Unfortunately, people made the same mistake Kahneman calls out in his taxicab example: ignoring the prevalence and assuming that test sensitivity is the probability of having antibodies, given a positive test. When it is really the reverse — the probability of getting a positive test, given you have antibodies.
This misconception led people to clamor for massive, indisciminate testing early in the epidemic when prevalence was low and indiscriminate testing would have given a large number of false positive results. (Whether tests for active infections, or antibody tests for prior infections.)
It also kept people from understanding the wisdom of preferentially testing people likely to have the virus. Persons with a fever and cough, or exposed to known cases, would have a much higher prevalence than the general population. And a much lower rate of false positives. If such people had a 35% prevalence, then with 99% sensitivity and specificity, a person testing positive would have a 98% chance of having the virus.
It was right to want some large-scale random testing of the population to determine prevalence. This works even when prevalence is low, since you can discount for false positives. It’s individual tests that have poor predictive value under those conditions.
This is not meant to excoriate the press or the public. Medical tests are often presented in confusing ways. Beyond that, "The way in which the PPV depends on the sensitivity, specificity, and prevalence rate is sufficiently involved to be counterintuitive for most people."
None of this is intended as medical advice. If you get a coronavirus test, either for an active infection or for antibodies, heed what your medical professional says, and do not try to second-guess him.
Finally, the discussion above assumes both test sensitivity and specificity are greater than zero and less than one. This is usually the case, but not always. To see what happens when sensitivity and specificity take on values of zero or 1, use the calculator.
