First of all, if you were a man, you were outta luck. The overall survival rate for men was 20%. For women, it was 74%, and for children, 52%. Yes, it was indeed "women and children first."

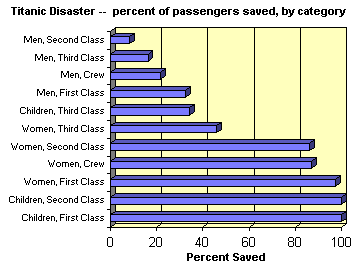
But what about class? Well, third class women were 41% more likely to survive than first class men. And third class men were twice as likely to survive as second class men.

Yes, class is a far weaker variable in determining survival rate than sex or age. Indeed, most of the variance in first class vs. third class survival rates can be attributed to sex alone. The reason for this is simple: 44% of the first class passengers were women, while only 23% of the third class passengers were women. Because the survival rate for women was far greater than the survival rate for men, we would thus expect a much higher survival rate for first class passengers as a whole than for third class passengers as a whole.

And sex and age differences aside, why would anyone be surprised that passengers in steerage would have a lower survival rate than passengers topside close to the boat deck? (For the findings of Lord Mersey's Enquiry regarding the survival rate for third class passengers, see below under Lord Mersey's Report.)

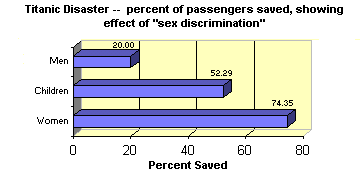
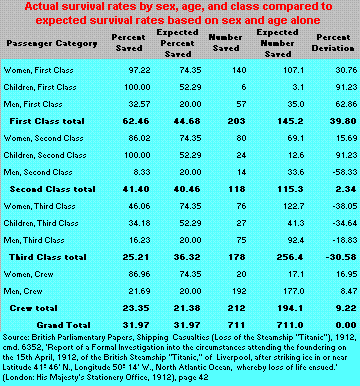
The table Actual survival rates by sex, age, and class compared to expected survival rates based on sex and age alone, clarifies the variance in survival rates associated with (but not necessarily caused by) class. If sex and age were the only variables determining probability of survival, we would expect women in each class to have a 74.35% chance of survival, children to have a 52.29% chance, and men to have a 20% chance. Applying these percentages to the actual number of women, children, and men in each class, we compute the expected number of survivors. We then compute how that number varies from the actual number of survivors for that sex, age, and class category.

This method shows that the expected overall survival rate for first class passengers was 44.68%, for second class 40.46%, for third class 36.32%, and for crew 21.38%. It also shows that the actual survival rate was 39.80% higher than expectation for first class as a whole, and 30.58% below expectation for third class as a whole.

The more primitive approach -- taken by most writers on this subject -- is to divide the first-class overall survival rate (62.46%) by the overall average survival rate (31.97%), conclude that first-class passengers were twice as likely to survive as the average passenger, and attribute all this variance to class. The folly of this approach is obvious.

And speaking of folly, those interested in further amusement can check out the article "It Was Sad," in The New Yorker, 10/14/96, p. 94. The author rambled on for several pages in an futile attempt to debunk what he called the "myth" of male heroism in the Titanic disaster. Since he had no factual basis for his beliefs, the effect was amazingly bad. For the source of some of the logical errors critiqued above, see articles on the Ecological Fallacy and Simpson's Paradox, both of which afflict popular analyses of quantitative data to an appalling degree. If you are interested in doing some survival analysis at the individual passenger level, see the Kaggle Titanic competition. (If I were doing it I would probably use a Gradient Boosting Machine solution, but it's way down my list of things to do. If you are interested, try it.)

Finally, please note that comparing the absolute number of survivors in various categories does not address the likelihood of survival for passengers in any given category. Thus, the following statements are all true:

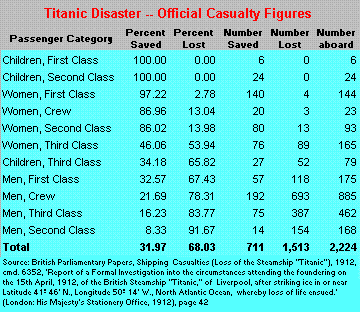
• "Among the survivors, third class children outnumbered first class children by a ratio of more than four to one."(True, but the survival rate for third class children was only 34.18%, compared to 100% [or maybe 85.71%, see note below on Helen Allison] for first class children. There were just a lot more children in third class.)
• "More men survived than women." (True, but only 20% of the men on board survived, compared to 74.35% of the women. Again, there were a lot more men on board than women.)
• "More than twice as many second class men survived as first class children." (Yup, it's true, but ALL the first class children survived, compared to only 8.33% of the second class men.)

Ridiculous observations, of course, but people actually say things like this. They do not address the central question of whether women and children received preferential treatment. As the numbers given above show, they unquestionably did.

---

Lord Mersey's Report

The casualty figures listed above are from Lord Mersey's Report (British Parliamentary Papers, Shipping Casualties (Loss of the Steamship "Titanic"), 1912, cmd. 6352, Report of a Formal Investigation into the circumstances attending the foundering on the 15th April, 1912, of the British Steamship "Titanic," of Liverpool, after striking ice in or near Latitude 41º 46' N., Longitude 50º 14' W., North Atlantic Ocean, whereby loss of life ensued. (London: His Majesty's Stationery Office, 1912). Lord Mersey's report is available in major libraries in the United States and elsewhere. The casualty figures appear on page 42 of the report. However, the "Titanic, Loss of the" article in the 13th edition of the Encyclopaedia Britannica, (London, 1926), also gives the casualty figures and is easier to find. (To answer a recurring question: although the Carpathia picked up 712 survivors, one of these died en route to New York and was counted among the casualties, reducing the total number of survivors to 711.)

One possible variance from the figures in Lord Mersey's report has been called to our attention. This concerns the loss of one child in first class, Miss Helen Lorraine Allison. For more information, see Encyclopaedia Titanica. Since this casualty, whether included or excluded, has no effect on the analysis, and we have not been able to review primary source material supporting it, we have elected to leave Lord Mersey's figures as they are. Clearly we will never know exactly how many people died in the wreck, since we do not know with absolute certainty how many people were on the ship in the first place.

Lord Mersey's report addressed (p. 40) the question of the low survival rate of third-class passengers, as follows:

"It has been suggested before the Enquiry that the third-class passengers had been unfairly treated; that their access to the boat deck had been impeded; and that when at last they reached that deck the first and second-class passengers were given precedence in getting places in the boats. There appears to have been no truth in these suggestions. It is no doubt true that the proportion of third-class passengers saved falls far short of the proportion of the first and second class, but this is accounted for by the greater reluctance of the third-class passengers to leave the ship, by their unwillingness to part with their baggage, by the difficulty in getting them up from their quarters, which were at the extreme ends of the ship, and by other similar causes. The interests of the relatives of some of the third-class passengers who had perished were in the hands of Mr. Harbinson, who attended the Enquiry on their behalf. He said at the end of his address to the court: 'I wish to say distinctly that no evidence has been given in the course of this case which would substantiate a charge that any attempt was made to keep back the third-class passengers ... I desire further to say that there is no evidence that when they did reach the boat deck there was any discrimination practiced either by the officers or by the sailors in putting them into the boats.'

"I am satisfied that the explanation of the excessive proportion lost is not to be found in the suggestion that the third-class passengers were in any way unfairly treated. They were not unfairly treated."

The Enquiry found the Titanic's excessive speed to blame for the disaster:

"The Court, having carefully enquired into the circumstances of the above mentioned shipping casualty, finds, for the reasons appearing in the Annex hereto, that the loss of the said ship was due to collision with an iceberg, brought about by the excessive speed at which the ship was being navigated.

Dated this 30th day of July, 1912

MERSEY, Wreck Commissioner"

Which pretty well sums it up. Seriously, what kind of idiot would drive a ship at full speed at night through an ice field? That question was asked by John Erskine in his noted essay, The Moral Obligation to be Intelligent:

So we forget the shocking blunder of the charge of the Light Brigade, and proudly sing the heroism of the victims. Lest we flatter ourselves that this trick of defense has departed with our fathers — this reading of stupidity in terms of the tragic courage that endures its results — let us reflect that recently, after full warning, we drove a ship at top speed through a field of icebergs. When we were thrilled to read how superbly those hundreds died, in the great English way, a man pointed out that they did indeed die in the English way, and that our pride was therefore ill-timed; that all that bravery was wasted; that the tragedy was in the shipwreck of intelligence. That discouraging person was an Irishman.

For even more delightful reading, see the Full text of the court's recommendations with a view to promoting the safety of vessels and persons at sea, which greatly improved the safety of ocean travel.

For additional primary source information on the Titanic disaster, check out the Encyclopaedia Titanica.

---

Miscellaneous Questions Answered

1. What was the number and capacity of the lifeboats?

Total rated capacity was 1,178 (enough for 53% of the 2,201 persons on board). There were 20 boats in all: 14 lifeboats, each designed to carry 65 passengers; 2 emergency boats, each with a capacity of 40 passengers; and 4 Engelhardt (collapsible) boats, each capable of carrying 47 passengers.

2. How many lifeboats were launched, and what was their capacity?

All 14 lifeboats, the two emergency boats, and two of the Engelhardt boats were launched. These had a capacity of 1,084 passengers. Obviously, many boats were not loaded to full capacity. There were many reasons for this; at first, many women and children were simply unwilling to be lowered 65 feet from the boat deck to the water. Some of the men put in boats were put there simply to show it was safe, and allay the fears of other passengers. (The two Engelhardt boats that were not launched floated off when the Titanic sank, and were used as rafts.)

3. Why were men put in the boats, when not all women and children had been put off?

One reason has just been given in the answer to Question 2. Another is that there was enough lifeboat capacity for ALL women and children (534 persons total), AND 550 men as well. (Total capacity of the boats launched was 1,084.) This explains why, especially as the situation became more urgent, more men were put in the boats. Indeed, if the boat crews had loaded one man for each woman or child loaded, they could have expected to save all women and children, plus as many men. [I believe that if this approach been adopted from the start, the boats would have been loaded more rapidly, passenger fear would have been reduced as families were kept together, and far more lives would have been saved in the long run.]

4. What was the last distess signal sent?

The Titanic's last distress, sent in Intercontinental Morse Code, was:

CQD CQD SOS SOS CQD DE MGY MGY

"CQD" was the common international distress signal in use at the time; "SOS" was a newer distress signal. "DE" is the international code meaning "from", adopted from the French preposition of the same meaning. "MGY" was the Titanic's call signal. The signal was keyed by John G. Phillips, the Titanic's chief Marconi operator, using a spark transmitter. For general information on this aspect of the Titanic debacle, see Wireless communications and the Titanic disaster By David Barlow. For technical details of the Titanic's wireless installation, see The wireless installation of R.M.S. Titanic by Douglas A. Kerr